This version relates to the SmoothStep.io website.

1 About Shaders

OpenGL is a widespread method of drawing stuff on a screen. Many apps, games, and other programs use it to do the actual drawing part of what they do. That is, when a program has some object to draw then OpenGL is what is used to actually colour in some pixels on the screen.

In order to do this, OpenGL has to know two things:

1. Where to draw; that is, which pixels on the screen should be coloured in for the given object.

2. What to draw; that is, once we know which pixels should be coloured then we need to figure out the colour.

An OpenGL shader is responsible for doing this, and a shader therefore has two parts:

1. A vertex program which answers the question of where to draw, and

2. a fragment program which answers the question of what to draw.

This website is concerned with the second of these, the fragment program, but to understand that we need to know a little about the first as well.

As the name suggests, the vertex program works by outlining a polygon on the screen by setting its vertices. The polygons used are usually triangles but some versions of OpenGL allow for quadrilaterals as well. As far as this website is concerned, the vertex program sets up a rectangle on the webpage and the fragment program will draw inside this rectangle.

What the vertex program also does is place some data at each vertex of the region. That data is then interpolated into the drawing region and can be used by the fragment program when deciding the colour of a pixel. As a simple example, the vertex program can put a colour at each vertex. Then it is as if that colour spreads out into the rectangle, blending with the colours at the other corners as it goes.

The fragment program then looks at each pixel in turn and decides what colour to put at that pixel. To make that decision, it can use the interpolated information from the vertex program together with other information given to it by the program that started the drawing process.

This website allows you to edit the core part of the fragment program to gain a little experience with what it does.

2 Basic Syntax

The end result of the code that you type into the text box is to set the colour of a pixel on the screen. Colours on computers are usually specified by mixing a certain amount of red, green, and blue. They can then be made partially transparent. In OpenGL, the ranges for these are from $0$ to $1$.

Task One: Basic Colours

Replace the code in the box with the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec4 c = vec4(1.0,1.0,1.0,1.0);
  fragColor = c;
}

Click Reload to see what this does.

Some important things to note from this:

1. Every line ends with ;

2. The last line will always be of the form fragColor = ...

3. Whole numbers are written as decimals; e.g., $1.0$

Try changing the numbers in the first line to see what happens (remember that they must be between $0$ and $1$). You must use a decimal point even if you use $0$ or $1$, so write these as $0.0$ and $1.0$ respectively. Vary one number at a time to see its effect.

vec4 c = vec4(1.0,1.0,1.0,1.0);

Task Two: Using a Picture

The fragment program can also read information from pictures. In OpenGL, a picture is referred to as a texture. On this website, you can choose textures via the Textures tab at the bottom.

Replace the code in the text box with the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

You can choose different images via the menu. The result should update when the image is changed.

There are several new things in this code.

• iTexture0 this refers to the picture that you've selected in the menu.

• texture(...) this looks up a particular point in the picture and returns the colour at that position. The point is specified by a vec2 which can be thought of as the coordinates of a point. The picture is considered to fill the "unit square" (even if it isn't a square), meaning that both the $x$ and $y$ coordinates should run from $0$ to $1$.

• fragCoord contains the location of a point in the output rectangle on the screen.

• iResolution is the size of the output rectangle, dividing by it converts the position coordinates so that they range from $0$ to $1$ and therefore can be fed to the texture command.

Task Three: Mixing Colour and Texture

Copy the following

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  c *= vec4(1.,0.,0.,1.);
  fragColor = c;
}

Click Build to see what this does. Try changing the numbers in the vec4. Leave the fourth one as 1. and remember that the others have to be between $0$ and $1$, and they must always have a decimal point.

Other ways of combining the colours are:

• c += vec4(...)

• c -= vec4(...)

• c /= vec4(...)

  This works best when the first three numbers in the fixed colour are small. Try vec4(0.1,0.1,0.1,1.0)

There are other, more sophisticated, methods of combining colours which we'll explore in later sections.

Task Four: Colour Swapping

It is possible to access the components of a colour individually or in groups. Replace the code in the box with the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  c.rgb = c.gbr;
  fragColor = c;
}

The r, g, and .b refer to the red, green, and blue components of the colours. There's a fourth one, a, which refers to the transparency (known as the alpha). The code above says "set the red to whatever the green was originally, the green to whatever the blue was originally, and the blue to whatever the red was originally". The rules in using them are:

1. The lengths of the strings of letters must be the same.

2. There can be repetitions on the right-hand side but not on the left-hand side.

Task Five: Modifying a Picture

Replace the code in the text box with the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx += vec2(0.5,0.5);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

Just as vec4 refers to a list of four numbers and is used to represent a colour, so vec2 refers to a list of two numbers and is used to represent a position.

The above adds $0.5$ to both the $x$–coordinates and $y$–coordinates of the look-up position. So at a point, say $(0.2,0.3)$, it actually looks at the colour on the image at $(0.7,0.8)$. This has the effect of moving the image down and to the left.

What is worth noting here is what happens in the other quadrants. At, say, $(0.7,0.3)$ then the program is looking at $(1.2,0.3)$. This is outside the picture, so what happens is the $1.2$ gets replaced by $0.2$ and so it looks up the colour at the position $(0.2,0.3)$.

Task Six: Zooming In

Replace the code in the text box with the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx -= vec2(0.5,0.5);
  tx /= 2.;
  tx += vec2(0.5,0.5);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

How would you describe the effect of this? Try changing the numbers to see if your description is accurate (make sure that the two occurrences of vec2(0.5,0.5) stay the same as each other).

3 Mathematics

The various things that the fragment program works with all consist of numbers or lists of numbers. Therefore, one can do standard mathematical stuff with them. There are also several functions that prove very useful in fragment programs.

Task Seven: Interpolating Pictures

Pick a second texture (which will be called iTexture1). Choose two different images for the two textures.

Replace the code in the text box with the following, make sure the $1.0$ in the last line has its decimal point:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  vec4 c1 = texture(iTexture1, tx);
  fragColor = mix(c1,c,tx.x);
}

There's not a lot to experiment with here. Try changing the images, and you could swap c and c1 in the last line.

Task Eight: Smoothly Interpolating Pictures

The above interpolates linearly between the two pictures. Depending on the pictures, the place at which the images are obviously mixing can be quite close to the edges. We can make a slightly more complicated version of the above to concentrate the mixing in the centre.

Make sure you have at least two textures, and replace the code in the text box with the following (as before, watch out for the decimal points):

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  vec4 c1 = texture(iTexture1, tx);
  float t = pow(tx.x,2.0) * (3.0 * tx.x - 2.0);
  fragColor = mix(c1,c,t);
}

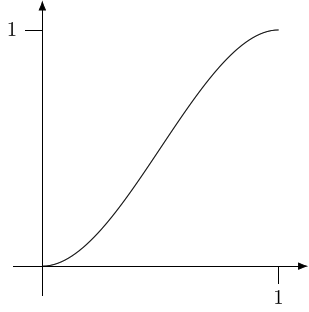
The key here is the formula on the third line. In normal mathematical notation, this is:

The graph of this, for $0\le x\le 1$ is in Figure 1.

In this code, we've seen how to write powers. The code pow(tx.x,2.0) squares the value of tx.x.

Task Nine: Shifting a Picture

In Task Five:, we had the following code:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx += vec2(0.5,0.5);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

This shifts the picture down and to the left, and where a picture coordinate goes out of the range from $0$ to $1$ then it "wraps around". In mathematical terms, this is because the program takes the fractional part of the coordinates. We can do this explicitly using the fract function.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx += vec2(0.5,0.5);
  tx = fract(tx);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

The fract function throws away the whole number part of a number, leaving just the decimal part.

Other useful functions for changing the texture coordinates (and colours) are:

Another useful function is clamp. This is used to clamp one number between two others. For example, $clamp(t,0,1)$ will always return a number that is between $0$ and $1$. If $t$ is between $0$ and $1$ then it will return $t$, but if $t$ is below $0$ it will return $0$ and if $t$ is above $1$ it will return $1$.

Try the following:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx -= vec2(0.5,0.5);
  tx = abs(tx);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx = min( vec2(.9,.9),tx);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx = max( vec2(.1,.1),tx);
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  tx = clamp(t, vec2(.1,.1),vec2(.9,.9));
  vec4 c = texture(iTexture0, tx);
  fragColor = c;
}

4 Advanced Mixing

In Section 3 we saw some ways to mix two pictures. In this section, we'll see some more that offer more control.

Task Ten: Masks

With two pictures, one way to decide how to mix them is to use a mask. This acts like the tape that painters put down to protect some areas when decorating: the places where the tape was show the original colour and where it wasn't shows the new colour.

Using a mask requires three pictures: the two pictures to be mixed and the mask.

To use a mask to select between two pictures, we use the interpolation formula as explained in Task Eight: but with the mask colour instead of the texture coordinates.

With the following code, the two pictures are iTexture0 and iTexture1 while the mask is iTexture2.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  vec4 c1 = texture(iTexture1, tx);
  vec4 m = texture(iTexture2, tx);
  c = mix(c1,c,m);
  fragColor = c;
}

A standard extension is to include grey in the mask to indicate partial masking.

Task Eleven: Alpha Masks

With some pictures, the part that you want masked is (almost) always going to be the same. For these pictures it is possible to add the mask to the picture by making parts of it transparent. This is done using the alpha channel. Recall that OpenGL uses four numbers to specify a colour. Three of these are the red, green, and blue components of that colour. The fourth is the alpha component which specifies the transparency. This can be used in place of a mask.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 tx = fragCoord / iResolution.xy;
  vec4 c = texture(iTexture0, tx);
  vec4 c1 = texture(iTexture1, tx);
  c.rgb = mix(c.rgb,c1.rgb,c1.a);
  fragColor = c;
}

5 Further Experiments

We've only scratched the surface of what's possible with shaders, even with this restricted situation. Here are some more to play with.

Task Twelve: Squaring

If you know about complex numbers, this one does $z\mapsto z^2$.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  vec2 tx;
  tx.x = t.x * t.x - t.y * t.y;
  tx.y = 2.0 * t.x * t.y;
  tx /= 2.0;
  tx += 0.5;
  vec4 c = texture(iTexture0,tx);
  fragColor = c;
}

If you liked that one, try this:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  vec2 tx;
  tx.x = t.x * t.x * t.x - 3.0 * t.x * t.y * t.y;
  tx.y = 3.0 * t.x * t.x * t.y - t.y * t.y * t.y;
  tx /= 2.0;
  tx += 0.5;
  vec4 c = texture(iTexture0,tx);
  fragColor = c;
}

Task Thirteen: Droste

The Droste effect is where an image gets copied into itself. This is quite straightforward with shaders.

First, a circular one.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = length(t);
  t /= r;
  r = pow(2.0,-fract(-log2(r)));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

To change the focus, change the vec2(0.5,0.5) to something like vec2(0.3,0.6) both in the first line and near the end.

Next, square.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = max(abs(t.x), abs(t.y));
  t /= r;
  r = pow(2.0,-fract(-log2(r)));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

Or we could have a diamond.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = abs(t.x) + abs(t.y);
  t /= r;
  r = pow(2.0,-fract(-log2(r)));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

Task Fourteen: Escher

If you like the Droste effect, here's an Escherian spin on them.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = length(t);
  float th = atan(t.y,t.x)/6.28318530718;
  t /= r;
  r = pow(2.0,-fract(-log2(r) + th));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

Now with squares.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = max(abs(t.x),abs(t.y));
  float th = atan(t.y,t.x)/6.28318530718;
  t /= r;
  r = pow(2.0,-fract(-log2(r) + th));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

And finally, with diamonds.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 t = fragCoord / iResolution.xy;
  t = (t - vec2(.5,.5))*2.;
  float r = abs(t.x) + abs(t.y);
  float th = atan(t.y,t.x)/6.28318530718;
  t /= r;
  r = pow(2.0,-fract(-log2(r) + th));
  t *= r;
  t /= 2.0;
  t += vec2(0.5,0.5);
  vec4 c = texture(iTexture0,t);
  fragColor = c;
}

6 Some Technical Details